Differentiable Imaging


Advanced Physics Research, 2023


Advanced Devices & Instrumentation, 2025

Abstract

Differentiable Imaging is an innovative framework that seamlessly integrates optical hardware with computational algorithms to address critical challenges in traditional computational imaging. By leveraging differentiable programming and automatic differentiation, this approach enables end-to-end optimization of complete imaging systems while accounting for real-world hardware imperfections. The result is simplified hardware designs, enhanced imaging performance, and improved system robustness across diverse imaging modalities. The differentiable linkage among all system components ultimately enables genuine co-design in computational imaging.

Introduction

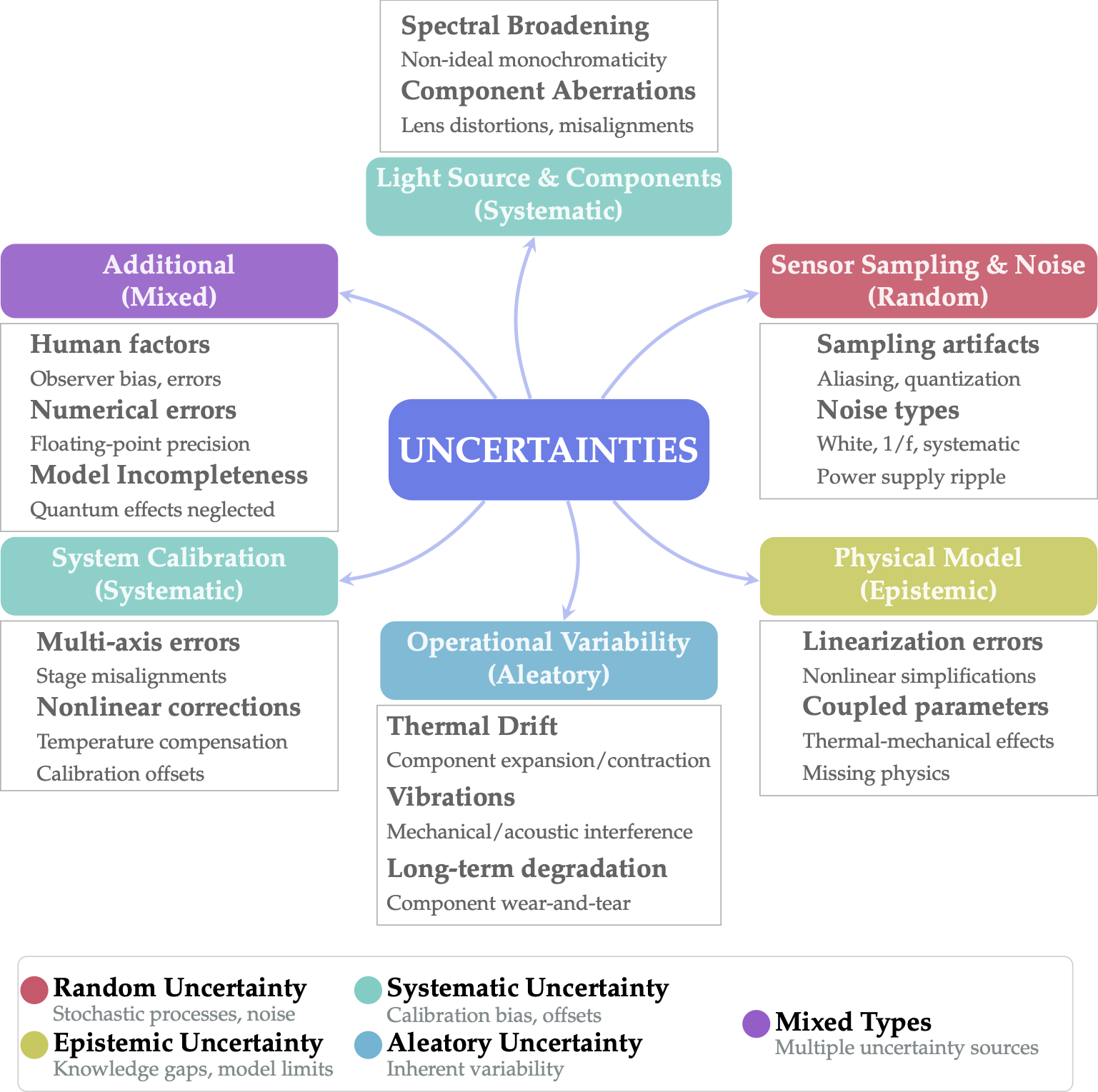
Sources of uncertainty in computational imaging systems
Uncertainties that lead to mismatch between real systems and numerical modeling.

Computational imaging has made significant advances but continues to face substantial challenges from system uncertainties. These uncertainties can be categorized into five key areas:

Effective co-design requires multi-variable optimization with accurate mathematical modeling of real systems. These uncertainties not only hinder precise numerical modeling but also complicate inverse problem solving, creating a fundamental bottleneck in computational imaging advancement.

Technical Framework

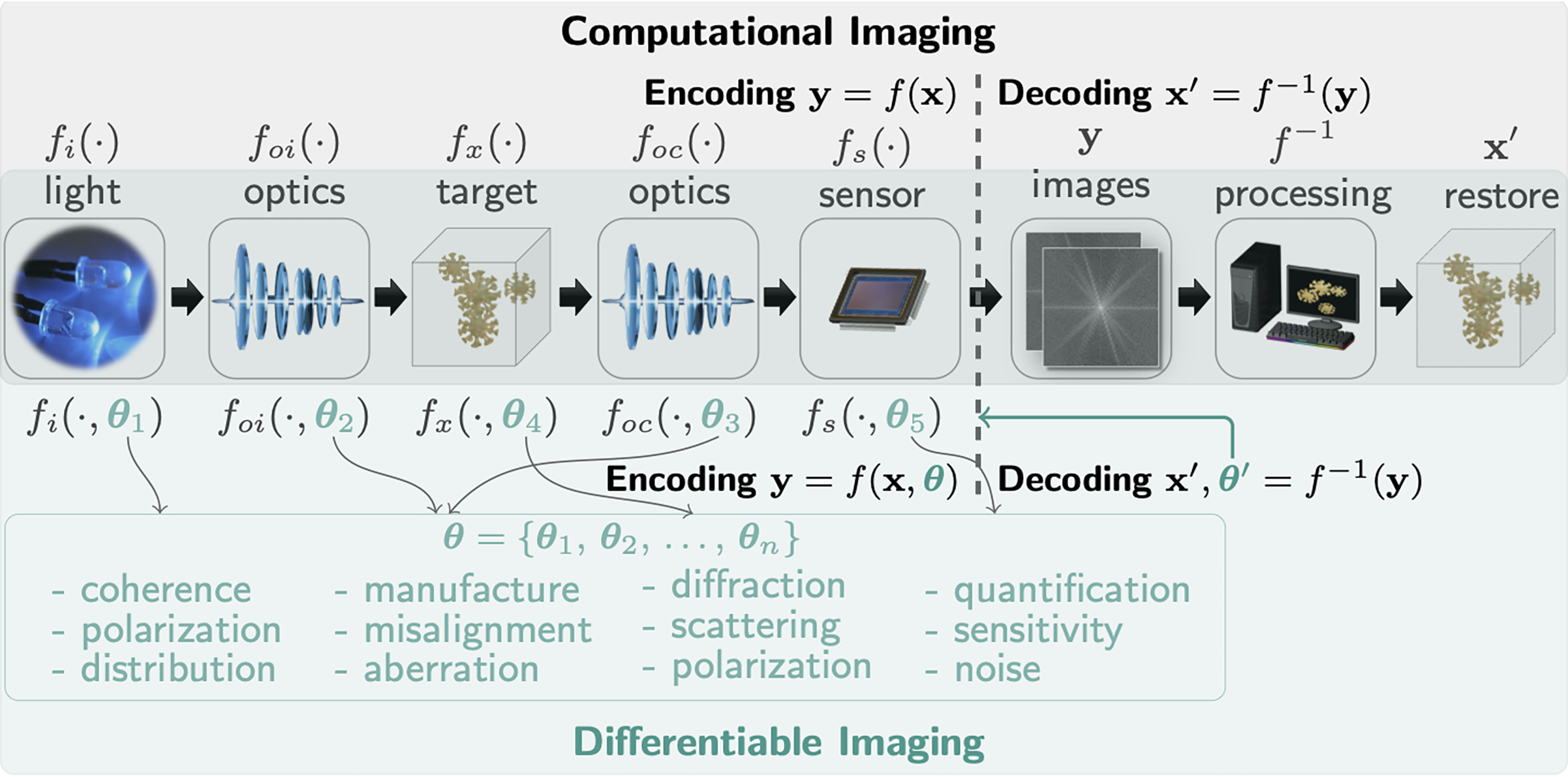
Differentiable imaging framework
Comparison of Computational Imaging and Differentiable Imaging.

Differentiable imaging 1 fundamentally redefines co-design by integrating physically accurate models within machine learning architectures for comprehensive end-to-end optimization. This framework specifically targets uncertainties that cause critical mismatches between real-world systems and their numerical representations. Through differentiable programming and automatic differentiation, these uncertainties are explicitly modeled and their impacts systematically mitigated.

The framework introduces two primary innovations:

  1. System Imperfection Modeling: Direct integration of hardware imperfections into imaging models (represented as f(x,θ) where θ encapsulates imperfection parameters)
  2. Differentiable Optimization: Implementation of inverse problem solving using differentiable optimization algorithms, enabling gradient-based optimization across the entire imaging pipeline

This integrated methodology facilitates closed-loop optimization, resulting in robust, high-performance imaging systems that maintain effectiveness despite real-world imperfections.

Research Achievements

Since 2021, our exploration of differentiable imaging across various domains has led to significant advancements:

Techniques Uncertainties Achievements
Differentiable Holography2,3 Defocus distance; Complex light-wave interaction; Single-shot wavefield imaging; high-density Single-shot 3D PIV
Differentiable Lensless Imaging4 Sensor scanning positions; defocus distances; Pixel-super resolution; High-performance imaging; Compact and cost-effective hardware
Uncertainty-Aware Fourier Ptychography5 Modelable: misalignment, element aberrations;
Statistical: noise, low quality data		 Simplified measurements; resolution beyond traditional physical limits; expanded system functions

Our research has revealed three fundamental principles:

  1. Precision in Modeling: The accuracy of optical system modeling is paramount to successful implementation
  2. Physics-Grounded Algorithms: Algorithms rooted in fundamental physical principles ensure computational efficiency, system robustness, and result interpretability
  3. System-Algorithm Synergy: Effective interplay between physical hardware and computational models is crucial for both imaging quality and optimal system design

Differentiable imaging holds potential for significant expansion beyond current applications. Future developments may include integration with digital twin technology and contributions to AI for Science initiatives 6, opening new paradigms for scientific discovery and technological innovation.

  1. Ni Chen, Liangcai Cao, Ting-Chung Poon, Byoungho Lee, Edmund Y. Lam, “Differentiable Imaging: A New Tool for Computational Optical Imaging,” Advanced Physics Research, 2023. ↩

  2. Ni Chen, Congli Wang, Wolfgang Heidrich, “∂H: Differentiable Holography,” Laser & Photonics Reviews, 2023. ↩

  3. Yang Wu, Jun Wang, Sigurdur Thoroddsen, Ni Chen*, “Single-Shot High-Density Volumetric Particle Imaging Enabled by Differentiable Holography,” IEEE Transactions on Industrial Informatics, 2024. ↩

  4. Ni Chen, Edmund Y. Lam, “Differentiable pixel-super-resolution lensless imaging,” Optics Letters, 2025. ↩

  5. Ni Chen, Yang Wu, Chao Tan, Liangcai Cao, Jun Wang, Edmund Y. Lam, “Uncertainty-Aware Fourier Ptychography,” Light, Science & Applications, 2025. ↩

  6. Ni Chen, David J. Brady, Edmund Y. Lam, “Differentiable Imaging: progress, challenges, and outlook,” Advanced Devices & Instrumentation, 2025. ↩